Recursion - base case
We've left one of the hardest concepts for last - recursion. Recursion does have some powerful applications, however compared to for loops, it's often harder to conceptualize as well as the latter being able to perform many of the same tasks; which it's is why it's often overlooked. One of the reasons recursion is still useful to know is it may provide faster runtime than a linear search, such as with a sorting algorithm. Many algorithms with graphs will also find use of recursion.
Recursion is when a function calls itself, hence 'recursive'. If a function keeps calling itself, an infinite loop will occur. That is why all recursive functions need a base case. A base case is some condition that will break the recursive calls. Let's take a look at what a recursive function might look like with print statements to help us know what depth we are currently at.
In the code that follows, the base case is the line with if count
== 0. It's at this point that the recursive calls will stop and
then start back-tracking up through previous calls.
Why did some prints display multiple times, and what is going on with the count? We call the function with a value of 2. When we get to the first print, nothing unusual has happened and the initial value is displayed. We skip the base case since the count doesn't satisfy it. Now we get to the recursive call. We call the function itself with a value that is decremented by one. Because we called a function, the interpreter will move on to that before continuing with the parent function, that is why the third print doesn't print just yet.
So now the function is called with a count of 1. In a similar manner as before, the conditional keeps getting skipped and recursion continues: count becomes 0 and we've now reached our base case.
What happens inside the base case? We call return, which prevents everything below it from executing, including another recursive call. We will now start returning to the parent functions.
We return to the prior/parent function where the count is 1. This function remembers where it was at, which was the recursive line. And so the next line is a print, hence a print of a value of 1. There is nothing left after this line, so the function returns None and proceeds up the stack. the function prior/parent now is the one with a count of 2. This is the initial call, completing the recursive function.
When a function is called, it is put on something termed a call stack. The initial caller is at the top of the stack. Recursive calls will be added to the bottom of the stack. It should be noted that only the block on the bottom of the stack is active. All other blocks will wait until their turn. When a function returns, it is removed from the stack and the next item on the stack becomes active.
Let's look at a diagram representing the step-by-step processes of the call-stack in the recursive function in the previous code editor.
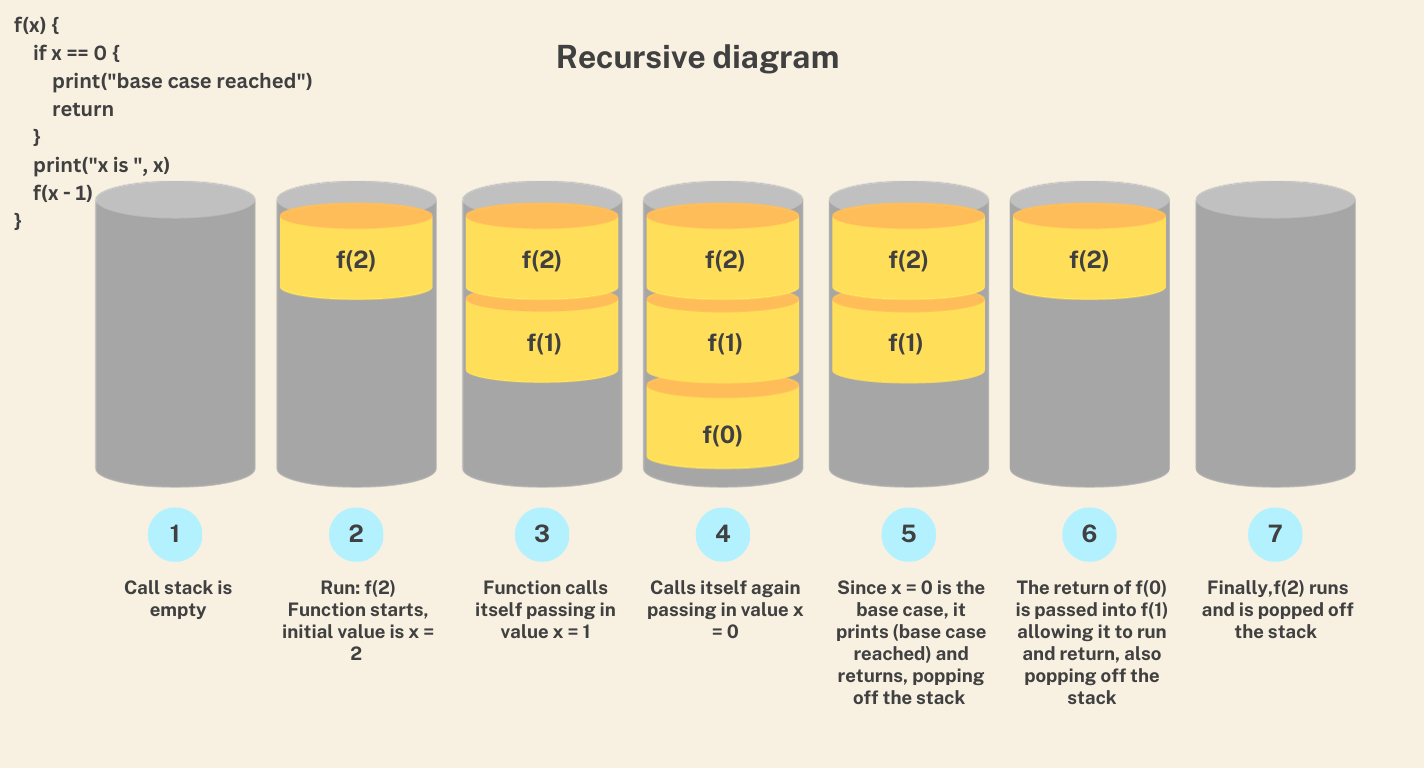
We add to the stack until we reach the base case. Once the base case is reached, the call stack will remove blocks, starting with those on the bottom. Up until we return back to the initial caller!