We will conclude the recursion section by looking at one case where it is particularly useful, trees. In programming, a tree is a hierarchical collection of nodes with edges connecting them. Nodes are a data structure, that at its simplest is an object with a value and a pointer to another node. There is a particular type of tree structure called a binary tree, where a node will have a value as well as a left and a right pointer to a child node. This kind of binary tree has multiple useful applications. From being efficient for searches, efficient for specific sorting algorithms, representing hierarchical data, and more.

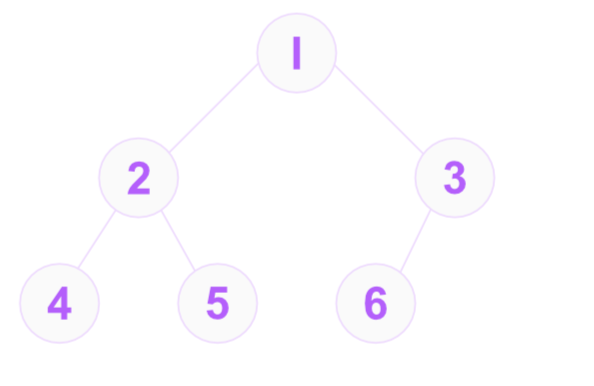
Let's see what a binary tree looks like in the diagram below. The node 1 is called the root node, it has two children nodes, 2 and 3. Then continuing, node 2 has two children nodes, 4 and 5, while node 3 has one child node, 6. Nodes 4, 5, and 6 are called leaf nodes as they have no children nodes.

Here's what our nodes look like in code, we can also add a str function to help print a node.

One of the classical and fundamental software engineering problems, is the challenge of finding all paths from the root of the tree down to its children nodes. Iterating through the tree won't work as even if the nodes exist in a list (which they might not), the order of this list won't correspond with the paths we need to take to go from root to children. So let's approach this problem from a recursive perspective.

To start, we should recognize a somewhat perplexing situation for function parameters in Python. Scalars are passed by value while objects are passed by reference. What this means is that in the code below, a copy of a is seen by the function whereas a reference to b is seen. So that when we print them afterwards, a ignores what happened in the function wheareas b remembers.

Now that we know this, let's use it to our advantage. We will use two arrays, one for the current path from root to child, and another to keep track of all of the paths seen. We use a base case that stops recursion when a node past a child is attempted to be used. Because both path and all_paths are passed by reference, if we want to record the current path we need to actually make a copy of it before adding, otherwise all of the paths would look the same at the end. There is one more gotcha in the final line that deletes a node value from a path. Because tree recursion involves walking up and down nodes in a tree, some paths will walk through the same node multiple times. To avoid this, we can delete a node from a path after we've walked through it.

Using the tree in the diagram above, our path through the whole tree looks like this: 1->2->4->2->5->2->1->3->6. And in more words if we separate it by when we turn around on the path

• (walk down) 1->2->4
• (walk up) 4->2
• (walk down) 2->5
• (walk up) 5->2->1
• (walk down) 1->3->6
• (walk up) 6->3->1

Practice Question

Use the tree from above and the code from below to answer the following questions.

def func(node, depth, target_depth): if not node: return 0 if depth == target_depth: return node.value return func(node.left, depth+1, target_depth) + \ func(node.right, depth+1, target_depth) func(root, 0, depth)

Q01.a. What does the code do?

Q01.b. Which line specifies the base case?

Submit

score: 0%

Show solution Show solution

---

Recursion definitely has its uses while at the same time having some limitations. For example, recursion past a certain point will result in a max depth exceeded error. So recursion of say the friends on Facebook would be computationally expensive. Additionally some parts of recursion are harder than normal, such as knowing what the base case should be as well as how to save the result. One more caveat is that sometimes a for loop can work just as well, say given a tree that requires traversal over all the nodes to perform some computation.

In the intermediate level we will cover this topic in more depth, describing its algorithm, complexity, and alternative traversal options.

With that said, recursion is still very powerful and we hope you find ways to use it!